Enjoying Gopher Basketball

Donate To GopherHole
TwistingMyMelon said:
I'm on your side, of course, but I'm not sure the team's overall performance is quite there yet to deserve another season. Five more wins: definitely; four more wins: quite likely; three more wins: maybe but grudgingly; two more wins: no.
Click to expand...
Who does he beat for those 3-4 wins with their remaining schedule?
 

RockChalk said:
Who does he beat for those 3-4 wins with their remaining schedule?
Click to expand...

As I've said before, I don't think that question is worth answering because, if you just look through a schedule and say "Well, I think we're probably better than three of these teams but worse than four and, considering the home/away factor, well, we'll go 3-4," I think you will end up being wrong more often than not.

That's why I gave the example of last season in a prior post. Looking at the schedule and the ratings of our conference opponents, we weren't good enough to beat anyone but we still beat three teams if you include the conference tournament game. There's not as much separating most of these teams as some people think and, on any given night, who knows? I'm pretty confident that we won't beat Purdue or Illinois on the road but there's enough of a chance in the others that on a good night it's possible.

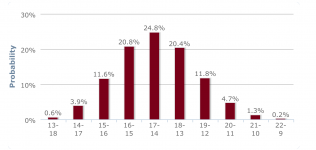
Just applying simple rules of mathematical probability (with a binomial distribution), you can't look at a series of games where you are the underdog (chance is < 50%) and assume you will lose all of them. For example, suppose you play four opponents and you have a 40% chance of beating each. The probability distribution of wins with those four trials is shown in the table below.

WINSProbability
0​
0.1296​
1​
0.3456​
2​
0.3456​
3​
0.1536​
4​
0.0256​
Total
1​

As you can see, your chances of winning none of those games is less than 13%. Your chances of winning 1 or 2 is actually about 69%.
 





USAF said:
LOL.

"Weakling Wednesday has advantages."

Good lord. Preposterous Statement Tournament number 1 seed.

BTW, maybe leave race out of it, numbnuts.
Click to expand...

Tell you what, if you never talk to me again, I'll never call you white trash again.
 


USAF said:
Hahahahahahahaha.

....


Hahahahahahahahahahahahahahahahahahahahahahahahahahahahahaha
Click to expand...
Ben's going to carelully thread the needle of "not finishing last" but making sure we're bad enough to get that sweet easy Weakling Wednesday win. His last two apologists will be thrilled.
 




TwistingMyMelon said:
As I've said before, I don't think that question is worth answering because, if you just look through a schedule and say "Well, I think we're probably better than three of these teams but worse than four and, considering the home/away factor, well, we'll go 3-4," I think you will end up being wrong more often than not.

That's why I gave the example of last season in a prior post. Looking at the schedule and the ratings of our conference opponents, we weren't good enough to beat anyone but we still beat three teams if you include the conference tournament game. There's not as much separating most of these teams as some people think and, on any given night, who knows? I'm pretty confident that we won't beat Purdue or Illinois on the road but there's enough of a chance in the others that on a good night it's possible.

Just applying simple rules of mathematical probability (with a binomial distribution), you can't look at a series of games where you are the underdog (chance is < 50%) and assume you will lose all of them. For example, suppose you play four opponents and you have a 40% chance of beating each. The probability distribution of wins with those four trials is shown in the table below.

WINSProbability
0​
0.1296​
1​
0.3456​
2​
0.3456​
3​
0.1536​
4​
0.0256​
Total
1​

As you can see, your chances of winning none of those games is less than 13%. Your chances of winning 1 or 2 is actually about 69%.
Click to expand...
Where is their best chance to win a freakin game? For god sake man, put yourself out there, no one is going to hold your feet to the fire.

Against those teams remaining on their schedule where do you see their best chance for a W?

I'll even simplify it a bit more, look at home or away, or maybe more talent or less talent, etc.
 

RockChalk said:
Where is their best chance to win a freakin game? For god sake man, put yourself out there, no one is going to hold your feet to the fire.

Against those teams remaining on their schedule where do you see their best chance for a W?

I'll even simplify it a bit more, look at home or away, or maybe more talent or less talent, etc.
Click to expand...

Easiest Remaining Games​

DateOpponentLocWin Odds
3/2Penn StHome65.2%
2/18RutgersHome63.7%
3/6IndianaHome62.1%
2/22Ohio StHome50.9%
2/3NorthwesternHome47.6%
2/6Michigan StHome28.7%
2/25NebraskaAway27.6%
3/9NorthwesternAway25.2%
2/11IowaAway21.7%
2/28IllinoisAway10.0%
 

RockChalk said:
Where is their best chance to win a freakin game? For god sake man, put yourself out there, no one is going to hold your feet to the fire.

Against those teams remaining on their schedule where do you see their best chance for a W?

I'll even simplify it a bit more, look at home or away, or maybe more talent or less talent, etc.
Click to expand...

I don't take any pleasure in doing that. Sorry.

Anyway, Gold Vision has done a pretty good job above in listing individual estimated probabilities for 10 of our remaining games.
 






RockChalk said:
Who does he beat for those 3-4 wins with their remaining schedule?
Click to expand...
I’ll give it a shot.

Indiana
Ohio State
Penn State
Rutgers

And if they only win a couple of those (which would be extremely disappointing) there are other reasonable opportunities, including Northwestern tomorrow and @ Iowa.
 


SelectionSunday said:
I’ll give it a shot.

Indiana
Ohio State
Penn State
Rutgers

And if they only win a couple of those (which would be extremely disappointing) there are other reasonable opportunities, including Northwestern tomorrow and @ Iowa.
Click to expand...
Good list. They are going to spring at least one upset. We have competed with everyone so I think that bodes well.
 

howeda7 said:
Ben's going to carelully thread the needle of "not finishing last" but making sure we're bad enough to get that sweet easy Weakling Wednesday win. His last two apologists will be thrilled.
Click to expand...
I mean, it's going from hell to one of the lower levels of purgatory, and that's with the star power of Garcia, and who knows how long he'll stick around. Not where I want to be with this program.
 

You must log in or register to reply here.



Top Bottom